20. Forecasting an AR(1) Process#
GPU
This lecture was built using a machine with the latest CUDA and CUDANN frameworks installed with access to a GPU.
To run this lecture on Google Colab, click on the “play” icon top right, select Colab, and set the runtime environment to include a GPU.
To run this lecture on your own machine, you need to install the software listed following this notice.
!pip install numpyro jax arviz
This lecture describes methods for forecasting statistics that are functions of future values of a univariate autoregressive process.
The methods are designed to take into account two possible sources of uncertainty about these statistics:
random shocks that impinge on the transition law
uncertainty about the parameter values of the AR(1) process
We consider two sorts of statistics:
prospective values \(y_{t+j}\) of a random process \(\{y_t\}\) that is governed by the AR(1) process
sample path properties that are defined as non-linear functions of future values \(\{y_{t+j}\}_{j \geq 1}\) at time \(t\)
Sample path properties are things like “time to next turning point” or “time to next recession”.
To investigate sample path properties we’ll use a simulation procedure recommended by Wecker [Wecker, 1979].
To acknowledge uncertainty about parameters, we’ll deploy numpyro to construct a Bayesian joint posterior distribution for unknown parameters.
Let’s start with some imports.
import matplotlib.pyplot as plt
import seaborn as sns
from typing import NamedTuple
# numpyro
import numpyro
import numpyro.distributions as dist
from numpyro.infer import MCMC, NUTS
# jax
import jax
import jax.random as random
import jax.numpy as jnp
from jax import lax
# arviz
import arviz as az
sns.set_style('white')
colors = sns.color_palette()
key = random.PRNGKey(0)
20.1. A Univariate First-Order Autoregressive Process#
Consider the univariate AR(1) model:
where the scalars \(\rho\) and \(\sigma\) satisfy \(|\rho| < 1\) and \(\sigma > 0\); \(\{\epsilon_{t+1}\}\) is a sequence of i.i.d. normal random variables with mean \(0\) and variance \(1\).
The initial condition \(y_{0}\) is a known number.
Equation (20.1) implies that for \(t \geq 0\), the conditional density of \(y_{t+1}\) is
Further, equation (20.1) also implies that for \(t \geq 0\), the conditional density of \(y_{t+j}\) for \(j \geq 1\) is
The predictive distribution (20.3) assumes that the parameters \(\rho, \sigma\) are known, which we express by conditioning on them.
We also want to compute a predictive distribution that does not condition on \(\rho,\sigma\) but instead takes account of our uncertainty about them.
We form this predictive distribution by integrating (20.3) with respect to a joint posterior distribution \(\pi_t(\rho,\sigma | y^t)\) that conditions on an observed history \(y^t = \{y_s\}_{s=0}^t\):
Predictive distribution (20.3) assumes that parameters \((\rho,\sigma)\) are known.
Predictive distribution (20.4) assumes that parameters \((\rho,\sigma)\) are uncertain, but have a known probability distribution \(\pi_t(\rho,\sigma | y^t )\). Notice the second equality follows because \(\{y_t\}\) is an AR(1) process when \((\rho, \sigma)\) are given.
We also want to compute some predictive distributions of “sample path statistics” that might include, for example
the time until the next “recession”,
the minimum value of \(Y\) over the next 8 periods,
“severe recession”, and
the time until the next turning point (positive or negative).
To accomplish that for situations in which we are uncertain about parameter values, we shall extend Wecker’s [Wecker, 1979] approach in the following way.
first simulate an initial path of length \(T_0\);
for a given prior, draw a sample of size \(N\) from the posterior joint distribution of parameters \(\left(\rho,\sigma\right)\) after observing the initial path;
for each draw \(n=0,1,...,N\), simulate a “future path” of length \(T_1\) with parameters \(\left(\rho_n,\sigma_n\right)\) and compute our “sample path statistics”;
finally, plot the desired statistics from the \(N\) samples as an empirical distribution.
20.2. Implementation#
First, we’ll simulate a sample path from which to launch our forecasts.
In addition to plotting the sample path, under the assumption that the true parameter values are known, we’ll plot \(0.9\) and \(0.95\) coverage intervals using conditional distribution (20.3) described above.
We’ll also plot a bunch of samples of sequences of future values and watch where they fall relative to the coverage interval.
class AR1(NamedTuple):
"""
Represents a univariate first-order autoregressive (AR(1)) process.
Parameters
----------
ρ : float
Autoregressive coefficient, must satisfy |ρ| < 1 for stationarity.
σ : float
Standard deviation of the error term.
y0 : float
Initial value of the process at time t=0.
T0 : int, optional
Length of the initial observed path (default is 100).
T1 : int, optional
Length of the future path to simulate (default is 100).
"""
ρ: float
σ: float
y0: float
T0: int
T1: int
def make_ar1(ρ: float, σ: float, y0: float, T0: int = 100, T1: int = 100):
"""
Factory function to create an AR1 instance with default values for T0 and T1.
Returns
-------
AR1
AR1 named tuple containing the specified parameters.
"""
return AR1(ρ=ρ, σ=σ, y0=y0, T0=T0, T1=T1)
Using the AR1 class, we can simulate paths more conveniently. The following function simulates an initial path with \(T0\) length.
def AR1_simulate_past(ar1: AR1, key=key):
"""
Simulate a realization of the AR(1) process for T0 periods.
Parameters
----------
ar1 : AR1
AR1 named tuple containing parameters (ρ, σ, y0, T0, T1).
key : jax.random.PRNGKey
JAX random key for generating random noise.
Returns
-------
initial_path : jax.numpy.ndarray
Simulated path of the AR(1) process and the initial y0.
"""
ρ, σ, y0, T0 = ar1.ρ, ar1.σ, ar1.y0, ar1.T0
# Draw εs
ε = σ * random.normal(key, (T0,))
# Set step function
def ar1_step(y_prev, t_ρ_ε):
ρ, ε_t = t_ρ_ε
y_t = ρ * y_prev + ε_t
return y_t, y_t
# Scan over time steps
_, y_seq = lax.scan(ar1_step, y0, (jnp.full(T0, ρ), ε))
# Concatenate initial value
initial_path = jnp.concatenate([jnp.array([y0]), y_seq])
return initial_path
Now we define the simulation function that generates a realization of the AR(1) process for future \(T1\) periods.
def AR1_simulate_future(ar1: AR1, y_T0, N=10, key=key):
"""
Simulate a realization of the AR(1) process for T1 periods.
Parameters
----------
ar1 : AR1
AR1 named tuple containing parameters (ρ, σ, y0, T0, T1).
y_T0 : float
Value of the process at time T0.
N: int
Number of paths to simulate.
key : jax.random.PRNGKey
JAX random key for generating random noise.
Returns
-------
future_path : jax.numpy.ndarray
Simulated N paths of the AR(1) process of length T1.
"""
ρ, σ, T1 = ar1.ρ, ar1.σ, ar1.T1
def single_path_scan(y_T0, subkey):
ε = σ * random.normal(subkey, (T1,))
def ar1_step(y_prev, t_ρ_ε):
ρ, ε_t = t_ρ_ε
y_t = ρ * y_prev + ε_t
return y_t, y_t
_, y = lax.scan(ar1_step, y_T0, (jnp.full(T1, ρ), ε))
return y
# Split key to generate different paths
subkeys = random.split(key, num=N)
# Simulate N paths
future_path = jax.vmap(single_path_scan, in_axes=(None, 0))(y_T0, subkeys)
return future_path
The following function plots the initial observed AR(1) path and simulated future paths along with predictive confidence intervals.
def plot_path(ar1, initial_path, future_path, ax, key=key):
"""
Plot the initial observed AR(1) path and simulated future paths,
along with predictive confidence intervals.
Parameters
----------
ar1 : AR1
AR1 named tuple containing process parameters (ρ, σ, T0, T1).
initial_path : array-like
Simulated initial path of the AR(1) process, shape(T0+1,).
future_path : array-like
Simulated future paths of the AR(1) process, shape (N, T1).
ax : matplotlib.axes.Axes
Matplotlib axes object to plot on.
key : jax.random.PRNGKey, optional
JAX random key for reproducible sampling.
Plots
-----
- Initial path (historical data)
- Multiple simulated future paths
- 90% and 95% predictive confidence intervals
- Expected future path
"""
ρ, σ, T0, T1 = ar1.ρ, ar1.σ, ar1.T0, ar1.T1
# Compute moments and confidence intervals
y_T0 = initial_path[-1]
j = jnp.arange(1, T1+1)
center = ρ**j * y_T0
vars = σ**2 * (1 - ρ**(2 * j)) / (1 - ρ**2)
# 95% CI
y_upper_c95 = center + 1.96 * jnp.sqrt(vars)
y_lower_c95 = center - 1.96 * jnp.sqrt(vars)
# 90% CI
y_upper_c90 = center + 1.65 * jnp.sqrt(vars)
y_lower_c90 = center - 1.65 * jnp.sqrt(vars)
# Plot
ax.plot(jnp.arange(-T0, 1), initial_path)
ax.axvline(0, linestyle='--', alpha=.4, color='k', lw=1)
# Choose 10 future paths to plot
index = random.choice(
key, jnp.arange(future_path.shape[0]), (10,), replace=False
)
for i in index:
ax.plot(jnp.arange(1, T1+1), future_path[i, :], color='grey', alpha=.5)
# Plot 90% and 95% CI
ax.fill_between(
jnp.arange(1, T1+1), y_upper_c95, y_lower_c95, alpha=.3, label='95% CI'
)
ax.fill_between(
jnp.arange(1, T1+1), y_upper_c90, y_lower_c90, alpha=.35, label='90% CI'
)
ax.plot(
jnp.arange(1, T1+1), center, color='red', alpha=.7, label='expectation'
)
ax.set_xlim([-T0, T1])
ax.set_xlabel("time", fontsize=13)
ax.set_ylabel("y", fontsize=13)
ax.legend(fontsize=8)
ar1 = make_ar1(ρ=0.9, σ=1, y0=10)
# Simulate
initial_path = AR1_simulate_past(ar1)
future_path = AR1_simulate_future(ar1, initial_path[-1])
# Plot
fig, ax = plt.subplots(1, 1)
plot_path(ar1, initial_path, future_path, ax)
plt.show()
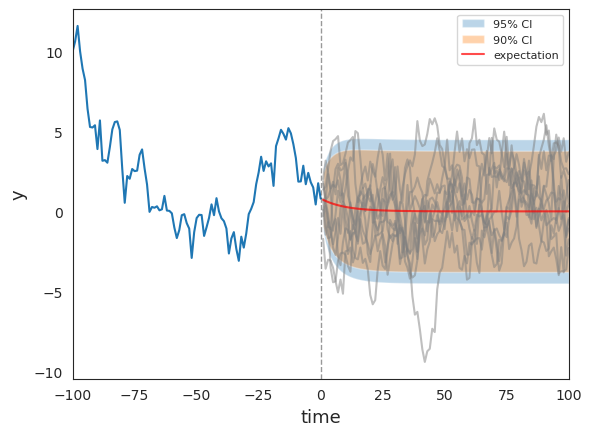
Fig. 20.1 Initial and predictive future paths#
As functions of forecast horizon, the coverage intervals have shapes like those described in https://python.quantecon.org/perm_income_cons.html
20.3. Predictive Distributions of Path Properties#
Wecker [Wecker, 1979] proposed using simulation techniques to characterize the predictive distribution of some statistics that are non-linear functions of \(y\).
He called these functions “path properties” to contrast them with properties of single data points.
He studied two special prospective path properties of a given series \(\{y_t\}\).
The first was time until the next turning point.
he defined a “turning point” to be the date of the second of two successive declines in \(y\).
For example, if \(y_t(\omega)< y_{t-1}(\omega)< y_{t-2}(\omega)\), then period \(t\) is a turning point.
To examine the time until the next turning point, let \(Z\) be an indicator process
Here \(\omega \in \Omega\) is a sequence of events, and \(Y_t: \Omega \rightarrow \mathbb{R}\) gives \(y_t\) according to \(\omega\) and the AR(1) process.
By Wecker’s definition, period \(t\) is a turning point, and \(Y_{t-2}(\omega) \geq Y_{t-3}(\omega)\) excludes the possibility that period \(t-1\) is a turning point.
Then the random variable time until the next turning point is defined as the following stopping time with respect to \(Z\):
In the following code, we name this statistic time until the next recession to distinguish it from another concept of turning point.
Moreover, the statistic time until the next severe recession is defined in a similar way, except the decline between periods is greater than \(0.02\).
Wecker [Wecker, 1979] also studied the minimum value of \(Y\) over the next 8 quarters, which can be defined as the random variable
It is interesting to study yet another possible concept of a turning point.
Thus, let
Define a positive turning point today or tomorrow statistic as
This is designed to express the event
“after one or two decreases, \(Y\) will grow for two consecutive quarters”
The negative turning point today or tomorrow \(N_t\) is defined in the same way.
Following [Wecker, 1979], we can use simulations to calculate probabilities of \(P_t\) and \(N_t\) for each period \(t\).
However, in the following code, we only use \(T_{t+1}(\omega)=1\) to determine \(P_t(\omega)\) and \(N_t(\omega)\), because we only want to find the first positive turning point.
20.4. A Wecker-Like Algorithm#
The procedure consists of the following steps:
index a sample path by \(\omega_i\)
from a given date \(t\), simulate \(I\) sample paths of length \(N\)
for each path \(\omega_i\), compute the associated value of \(W_t(\omega_i), W_{t+1}(\omega_i), \dots , W_{t+N}\)
consider the sets \(\{W_t(\omega_i)\}^{I}_{i=1}, \ \{W_{t+1}(\omega_i)\}^{I}_{i=1}, \ \dots, \ \{W_{t+N}(\omega_i)\}^{I}_{i=1}\) as samples from the predictive distributions \(f(W_{t+1} \mid y_t, y_{t-1}, \dots , y_0)\), \(f(W_{t+2} \mid y_t, y_{t-1}, \dots , y_0)\), \(\dots\), \(f(W_{t+N} \mid y_t, y_{t-1}, \dots , y_0)\).
20.5. Using Simulations to Approximate a Posterior Distribution#
The next code cells use numpyro to compute the time \(t\) posterior distribution of \(\rho, \sigma\).
Note that in defining the likelihood function, we choose to condition on the initial value \(y_0\).
def draw_from_posterior(data, size=10000, bins=20, dis_plot=1, key=key):
"""Draw a sample of size from the posterior distribution."""
def model(data):
# Start with priors
ρ = numpyro.sample('ρ', dist.Uniform(-1, 1)) # Assume stable ρ
σ = numpyro.sample('σ', dist.HalfNormal(jnp.sqrt(10)))
# Define likelihood recursively
for t in range(1, len(data)):
# Expectation of y_t
μ = ρ * data[t-1]
# Likelihood of the actual realization.
numpyro.sample(f'y_{t}', dist.Normal(μ, σ), obs=data[t])
# Compute posterior distribution of parameters
nuts_kernel = NUTS(model)
# Define MCMC class to compute the posteriors
mcmc = MCMC(
nuts_kernel,
num_warmup=5000,
num_samples=size,
num_chains=4, # plot 4 chains in the trace
progress_bar=False,
chain_method='vectorized'
)
# Run MCMC
mcmc.run(key, data=data)
# Get posterior samples
post_sample = {
'ρ': mcmc.get_samples()['ρ'],
'σ': mcmc.get_samples()['σ'],
}
# Plot posterior distributions and trace plots
if dis_plot == 1:
plot_data = az.from_numpyro(posterior=mcmc)
axes = az.plot_trace(
data=plot_data,
compact=True,
lines=[
("ρ", {}, ar1.ρ),
("σ", {}, ar1.σ),
],
backend_kwargs={"figsize": (10, 6), "layout": "constrained"},
)
return post_sample
post_samples = draw_from_posterior(initial_path)
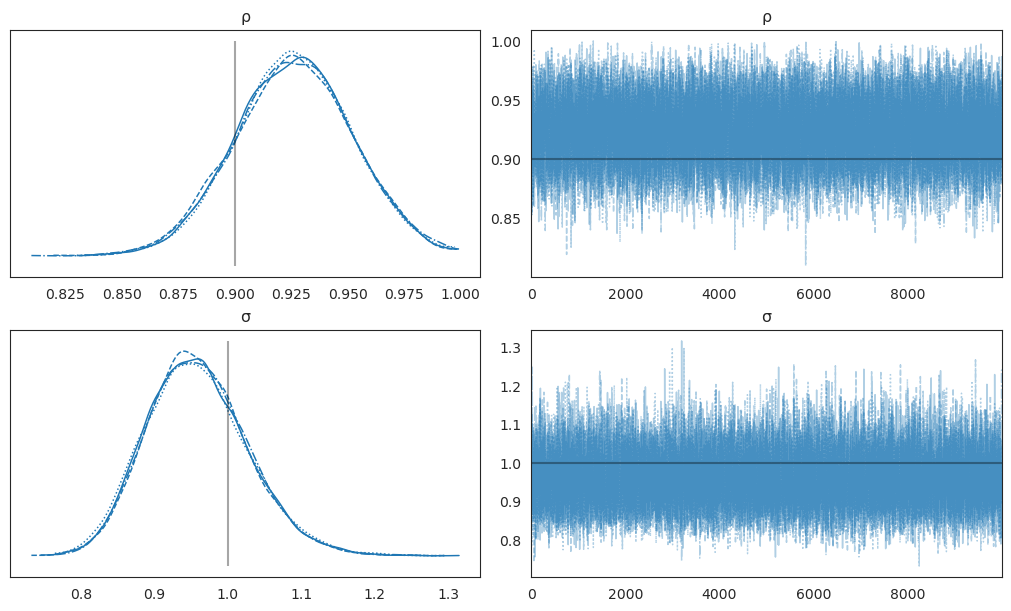
Fig. 20.2 AR(1) model#
The graphs above portray posterior distributions and trace plots. The posterior distributions (top row) show the marginal distributions of the parameters after observing the data, while the trace plots (bottom row) help diagnose MCMC convergence by showing how the sampler explored the parameter space over iterations.
20.6. Calculating Sample Path Statistics#
Our next step is to prepare Python code to compute our sample path statistics.
These statistics were originally defined as random variables with respect to \(\omega\), but here we use \(\{Y_t\}\) as the argument because \(\omega\) is implicit.
These two kinds of definitions are equivalent because \(\omega\) determines path statistics only through \(\{Y_t\}\).
Moreover, we ignore all equality in the definitions, as equality occurs with zero probability for continuous random variables.
def compute_path_statistics(initial_path, future_path):
"""Compute path statistics for the AR(1) process."""
# Concatenate the last two elements of initial path to identify recession
y = jnp.concatenate([initial_path[-3:], future_path])
n = y.shape[0]
def step(carry, i):
# identify recession
rec_cond = (y[i] < y[i-1]) & (y[i-1] < y[i-2]) & (y[i-2] > y[i-3])
# identify severe recession
sev_cond = (
(y[i] - y[i-1] < -0.02) & (y[i-1] - y[i-2] < -0.02) & (y[i-2] > y[i-3])
)
# identify positive turning point
up_cond = (
(y[i-2] > y[i-1]) & (y[i-1] > y[i]) & (y[i] < y[i+1]) & (y[i+1] < y[i+2])
)
# identify negative turning point
down_cond = (
(y[i-2] < y[i-1]) & (y[i-1] < y[i]) & (y[i] > y[i+1]) & (y[i+1] > y[i+2])
)
# Convert to int
rec = jnp.where(rec_cond, 1, 0)
sev = jnp.where(sev_cond, 1, 0)
up = jnp.where(up_cond, 1, 0)
down = jnp.where(down_cond, 1, 0)
return carry, (rec, sev, up, down)
_, (rec_seq, sev_seq, up_seq, down_seq) = lax.scan(step, None, jnp.arange(3, n-2))
# Get the time until the first recession
next_recession = jnp.where(
jnp.any(rec_seq == 1), jnp.argmax(rec_seq == 1) + 1, len(y)
)
next_severe_recession = jnp.where(
jnp.any(sev_seq == 1), jnp.argmax(sev_seq == 1) + 1, len(y)
)
# Minimum value in the next 8 periods
min_val_8q = jnp.min(future_path[:8])
# Get the time until the first turning point
next_up_turn = jnp.where(
jnp.any(up_seq == 1),
jnp.maximum(jnp.argmax(up_seq == 1), 1), # Exclude 0 return
len(y)
)
next_down_turn = jnp.where(
jnp.any(down_seq == 1),
jnp.maximum(jnp.argmax(down_seq == 1), 1),
len(y)
)
path_stats = (
next_recession, next_severe_recession, min_val_8q,
next_up_turn, next_down_turn
)
return path_stats
The following function creates visualizations of the path statistics in a subplot grid.
def plot_path_stats(next_recession, next_severe_recession, min_val_8q,
next_up_turn, next_down_turn, ax):
"""Plot the path statistics in subplots(3,2)"""
# ax[0, 0] is for paths of y
sns.histplot(next_recession, kde=True, stat='density', ax=ax[0, 1], alpha=.8)
ax[0, 1].set_xlabel("time until the next recession", fontsize=13)
sns.histplot(
next_severe_recession, kde=True, stat='density', ax=ax[1, 0], alpha=.8
)
ax[1, 0].set_xlabel("time until the next severe recession", fontsize=13)
sns.histplot(min_val_8q, kde=True, stat='density', ax=ax[1, 1], alpha=.8)
ax[1, 1].set_xlabel("minimum value in next 8 periods", fontsize=13)
sns.histplot(next_up_turn, kde=True, stat='density', ax=ax[2, 0], alpha=.8)
ax[2, 0].set_xlabel("time until the next positive turn", fontsize=13)
sns.histplot(next_down_turn, kde=True, stat='density', ax=ax[2, 1], alpha=.8)
ax[2, 1].set_xlabel("time until the next negative turn", fontsize=13)
20.7. Original Wecker Method#
Now we apply Wecker’s original method by simulating future paths and compute predictive distributions, conditioning on the true parameters associated with the data-generating model.
def plot_Wecker(ar1: AR1, initial_path, ax, N=1000):
"""
Plot the predictive distributions from "pure" Wecker's method.
Parameters
----------
ar1 : AR1
An AR1 named tuple containing the process parameters (ρ, σ, T0, T1).
initial_path : array-like
The initial observed path of the AR(1) process.
N : int
Number of future sample paths to simulate for predictive distributions.
"""
# Plot simulated initial and future paths
y_T0 = initial_path[-1]
future_path = AR1_simulate_future(ar1, y_T0, N=N)
plot_path(ar1, initial_path, future_path, ax[0, 0])
# Simulate future paths and compute statistics
def step(carry, n):
future_temp = future_path[n, :]
(next_reces, severe_rec, min_val_8q, next_up_turn, next_down_turn
) = compute_path_statistics(initial_path, future_temp)
return carry, (next_reces, severe_rec, min_val_8q, next_up_turn, next_down_turn)
_, (next_reces, severe_rec, min_val_8q, next_up_turn, next_down_turn
) = lax.scan(step, None, jnp.arange(N))
# Plot path statistics
plot_path_stats(next_reces, severe_rec, min_val_8q,
next_up_turn, next_down_turn, ax)
fig, ax = plt.subplots(3, 2, figsize=(15, 12))
plot_Wecker(ar1, initial_path, ax)
plt.show()
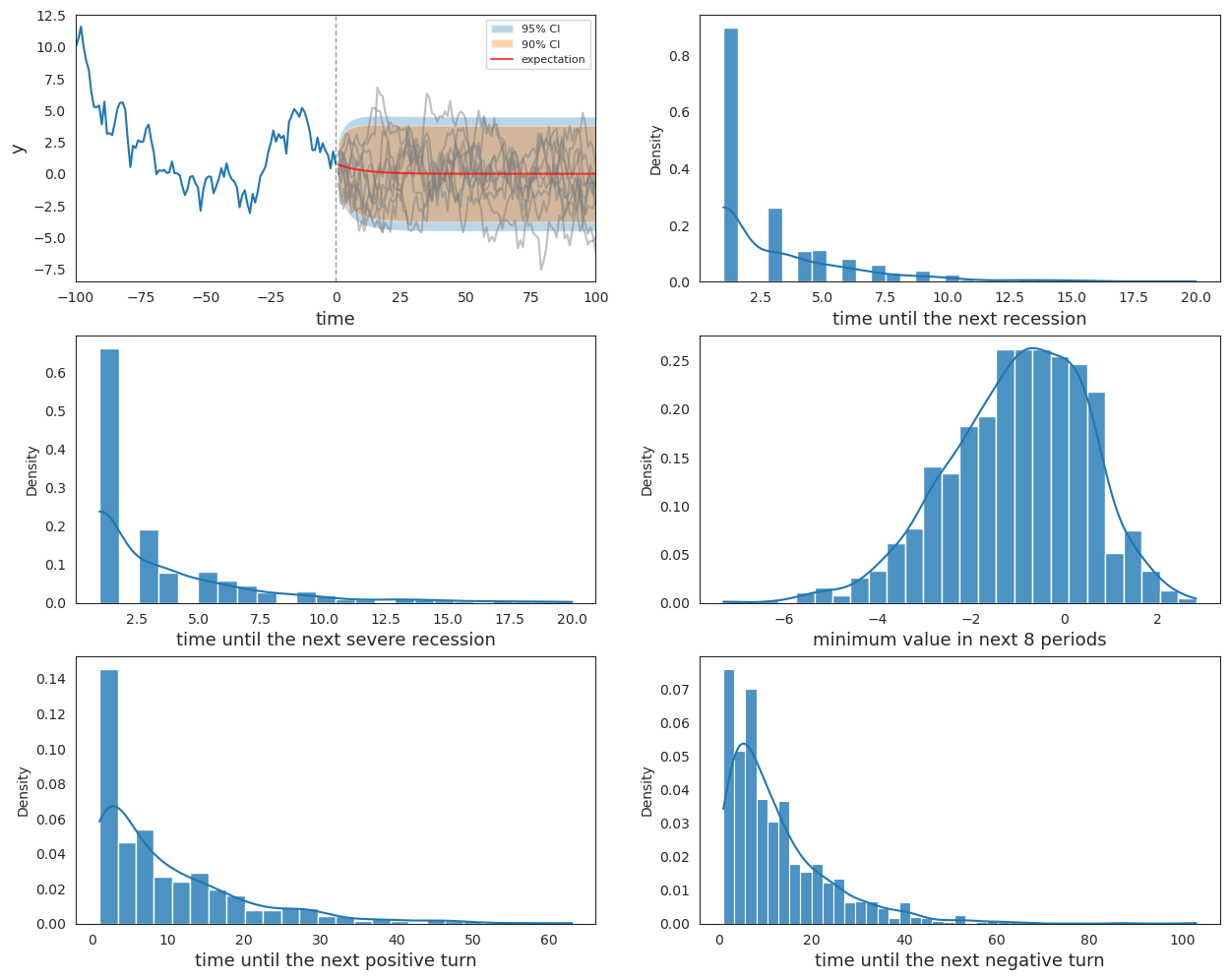
Fig. 20.3 Distributions of statistics by Wecker’s method#
20.8. Extended Wecker Method#
Now we apply our “extended” Wecker method based on predictive densities of \(y\) defined by (20.4) that acknowledge posterior uncertainty in the parameters \(\rho, \sigma\).
To approximate the integration on the right side of (20.4), we repeatedly draw parameters from the joint posterior distribution each time we simulate a sequence of future values from model (20.1).
def plot_extended_Wecker(
ar1: AR1, post_samples, initial_path, ax, N=1000
):
"""Plot the extended Wecker's predictive distribution"""
y0, T1 = ar1.y0, ar1.T1
y_T0 = initial_path[-1]
# Select a parameter sample
index = random.choice(
key, jnp.arange(len(post_samples['ρ'])), (N + 1,), replace=False
)
ρ_sample = post_samples['ρ'][index]
σ_sample = post_samples['σ'][index]
# Compute path statistics
subkeys = random.split(key, num=N)
def step(carry, n):
ar1_n = make_ar1(ρ=ρ_sample[n], σ=σ_sample[n], y0=y0, T1=T1)
future_temp = AR1_simulate_future(
ar1_n, y_T0, N=1, key=subkeys[n]
).reshape(-1)
(next_reces, severe_rec, min_val_8q, next_up_turn, next_down_turn
) = compute_path_statistics(initial_path, future_temp)
return carry, (future_temp, next_reces, severe_rec,
min_val_8q, next_up_turn, next_down_turn)
_, (future_path, next_reces, severe_rec, min_val_8q, next_up_turn, next_down_turn
) = jax.lax.scan(step, None, jnp.arange(N))
# Plot simulated initial and future paths
plot_path(ar1, initial_path, future_path, ax[0, 0])
# Plot path statistics
plot_path_stats(next_reces, severe_rec, min_val_8q,
next_up_turn, next_down_turn, ax)
fig, ax = plt.subplots(3, 2, figsize=(12, 15))
plot_extended_Wecker(ar1, post_samples, initial_path, ax)
plt.show()
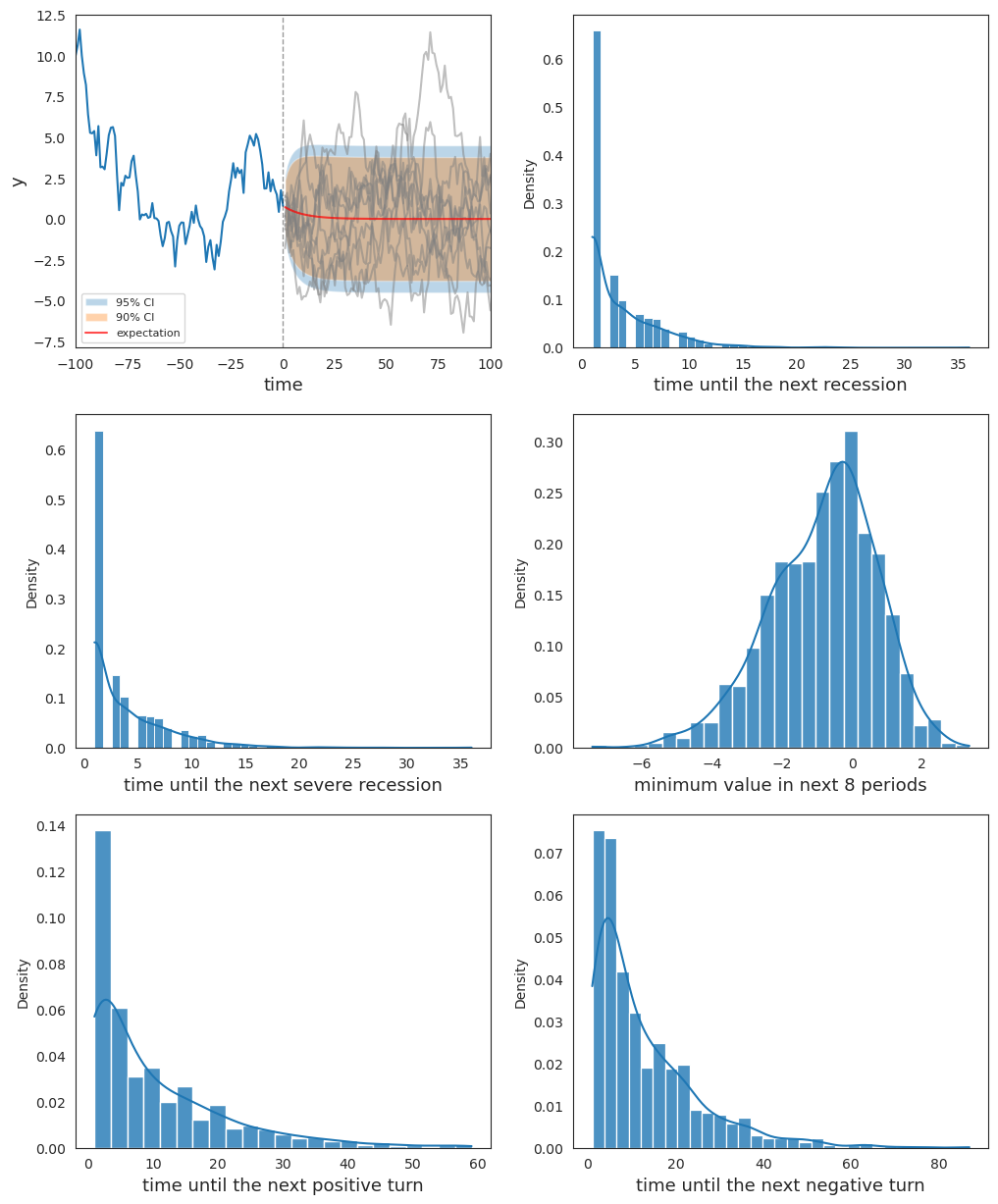
Fig. 20.4 Distributions of statistics by extended Wecker’s method#
20.9. Comparison#
Finally, we plot both the original Wecker method and the extended method with parameter values drawn from the posterior together to compare the differences that emerge from pretending to know parameter values when they are actually uncertain.
fig, ax = plt.subplots(3, 2, figsize=(12, 15))
plot_Wecker(ar1, initial_path, ax)
ax[0, 0].clear()
plot_extended_Wecker(ar1, post_samples, initial_path, ax)
plt.show()
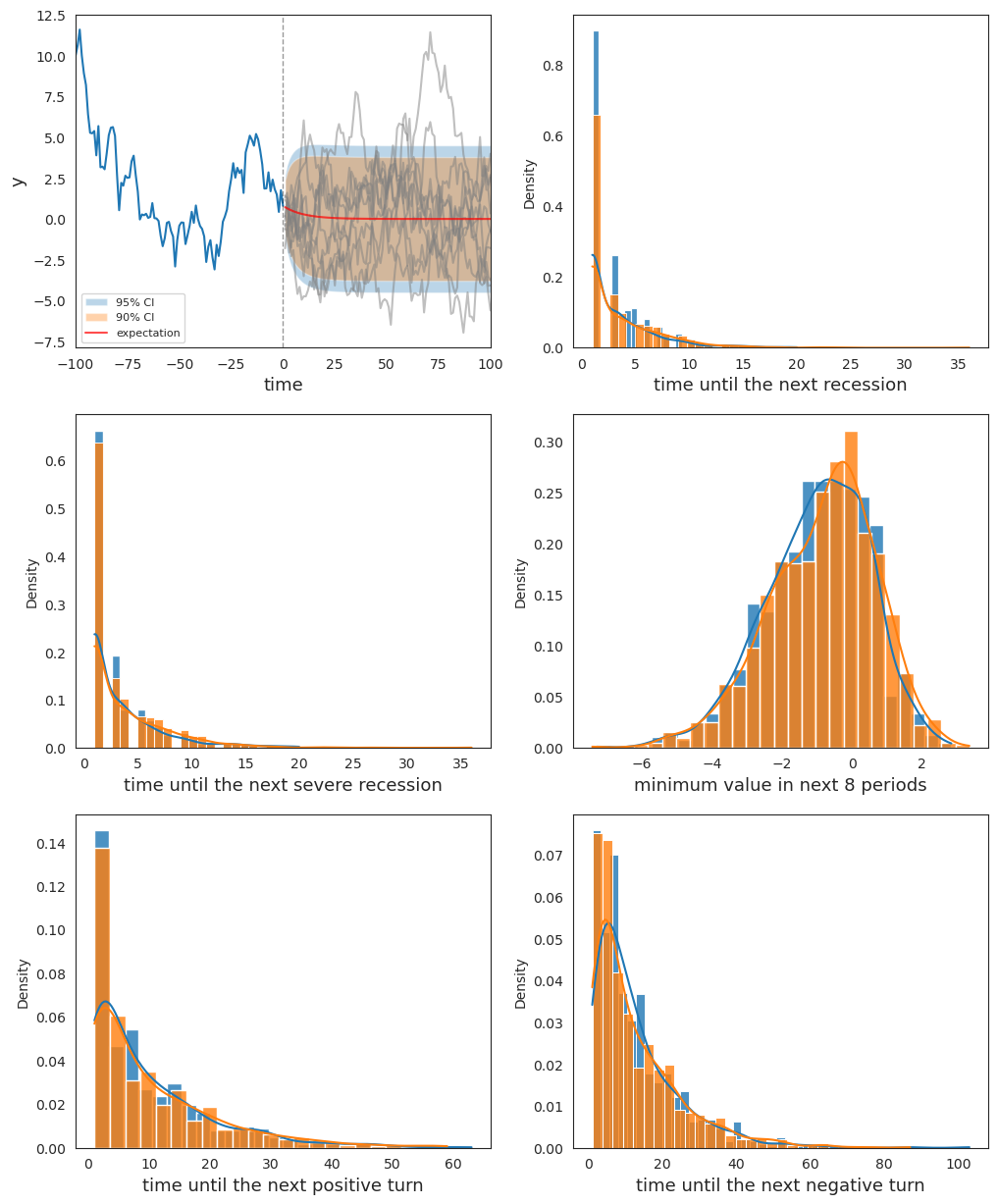
Fig. 20.5 Comparison between two methods#